import sisl as si
import numpy as np

%matplotlib inline
import matplotlib.pyplot as plt

Defining orbitals

Orbitals, and basis sets, is a complicated matter that requires a broader set of classes. sisl enables one to use orbitals without information, but also other specialized orbitals, such as atomic orbitals and Gaussian/Slater type orbitals. Information about the different orbitals can be found here.

---

In this tutorial we will show how one can create different orbitals, and use them.

orb = si.Orbital(1.2, q0=1)
print(orb)

Orbital{R: 1.20000, q0: 1.0}

All orbitals will have some idea of its range. I.e. the effective range at which it acts on something. The ranges are used in Geometry objects to estimate which atoms interacts with other atoms, and as such they are the back-bone of tight-binding models.

The above orbital has a range of 1.2 Ang, and an initial charge of 1 electron.

---

Orbitals with spherical shapes

Many other orbitals has some shape in real space. Here we will explore two such orbitals in sisl.

In this case we will populate the orbital with an exponential decaying shape (non-physical, but instructive).

Here we define the orbital range as the maximum R such that integral:

\[\int^R |f(r)| dr\]

contains \(99\%\) of the function.

r = np.linspace(0, 3, 200)
f = np.exp(-2 * r**2)
sorb = si.SphericalOrbital(1, (r, f), R={"contains": 0.99})
print(sorb)

SphericalOrbital{l: 1, R: 1.2879999999999991, q0: 0.0}

Now we have a spherical orbital with \(l=1\) quantum number. Lets plot its spherical form and its wavefunction:

for m in (0, 1):
    # Plotting for theta = phi = 45 angles
    plt.plot(r, sorb.psi_spher(r, 45, 45, m=m), label=f"m={m}")
plt.legend();

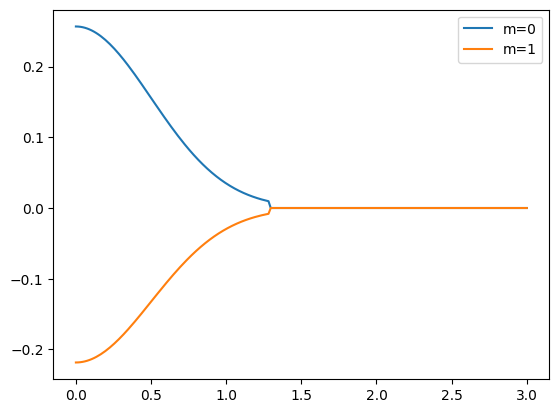
Note how the wavefunction gets truncated at the orbital radius, based on the truncation optimization.

---

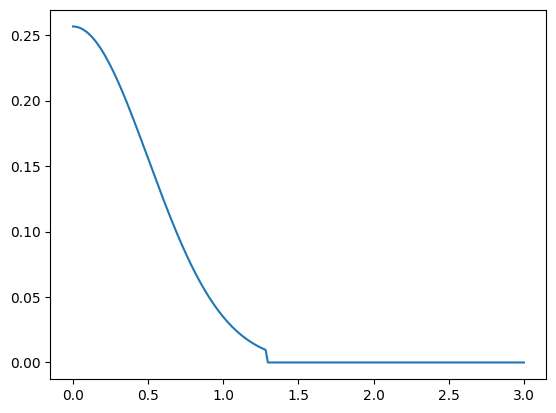
The SphericalOrbital is typically just a temporary orbital array used for creating proper atomic orbitals. Atomic orbitals contains relevant quantum numbers, but also a spherical function. The AtomicOrbital accepts many other possibilities of arguments, please refer to its documentation for detailed explanations.

aorb = si.AtomicOrbital("pz", spherical=sorb)
plt.plot(r, aorb.psi_spher(r, 45, 45));

Atoms with orbitals

Atoms are defined with 1 or more orbitals. To create an atom with a specific set of orbitals simply do:

C = si.Atom(6, [sorb, aorb])
print(C)

Atom{C, Z: 6, mass(au): 12.01070, maxR: 1.28800,
 SphericalOrbital{l: 1, R: 1.2879999999999991, q0: 0.0},
 AtomicOrbital{2pzZ1, q0: 0.0, SphericalOrbital{l: 1, R: 1.2879999999999991, q0: 0.0}}
}

This atom can then further be used in Geometry creations.